[ 6/25/2021 ] Labels: 04.Basic Study
Cello's resonance route in the body can be presumed by monitoring the locus of the sound at synchronized plural microphones. Pizzicato echoes are the best target of the measurement because they are formed by pure waveform and traceable.
To begin from the conclusion, the resonance route(groups) are roughly divided to four (tone) ranges.
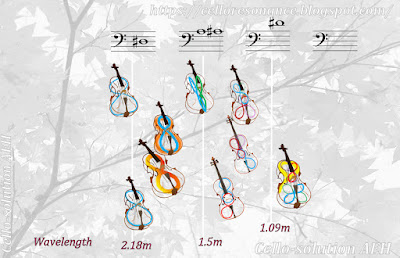
The tone around D#(156Hz) is really a very key. The wavelength of D#, 2.18 meter, is almost equivalent to the internal circumference of 4/4-cello body and the maximum length of 8-shape resonance orbit.
Slightly the upper pitch tones(:E-F,,) sometimes make a harsh interference wolf-tone against the echo( D#, dropped pitch ) of themselves just inside the bouts(body) wall.
At area[II], the resonance orbit is assumed taking as a single 8-shape orbit or a stable combination of two orbits.
At area[I], resonance wavelength shortens and the small 8-shape orbits can move to everywhere freely and elusive.
At area[III], the resonance route seems simply taking a double loop of area[II].
How be managed at area[IV]? There is no real single orbit of C,C#,D in upper area[III]. Fortunately wave-synthesis simulation program on MS-Excel can suggest us some hints.
For instance, cello's lowest tone C(66Hz, wavelength= 5.2 meter) can be described as an aggregation of the overtones(: E,G,C,), total length corresponds to 5.2 meter and shows similar wave-patterns. An overtone(:C131Hz) is not included.
The 8-shape orbit and the manner of resonance probably depends on the dimensions/structure of cello. We can recognize that the cello body has been an invention that can resonate to all pitches.
When a cello played with a bow, many noisy vibrations will be brought in. Unexpected resonance/interference will be brought by endpins too.
チェロのピチカート後の残響に注目して 筐体内での純粋な響きのルートを推定した。
結論的に言えば、図のⅠ,Ⅱ,Ⅲ,Ⅳの4つの領域に分けられるようだ。キーとなるのはD#音だ。4/4チェロの場合、D#(156Hz)付近の波長(=2.18m)がちょうど筐体内での(8の字のルートを描いた時の)最大の周長とほぼ等しい。つまりこれより高音の1オクターブ(Ⅱ領域)ではシングルな8の字軌道(または二つの8の字軌道の決まった組み合わせ)で任意の周波数の音を作ることができる。
D#より低い長周期波長(Ⅲ領域の1オクターブ)では2周することで任意の波長を得ることができる。D#(156Hz)のすぐ高音側に「ウルフトーン」の出現するエリア(E-F音)がある。直進する音波が筐体のフェンスの内側にピッチを下げエコーとして残留し、生成される最新のE-F音と激しく干渉するためである。
高音 Ⅰ領域では波長は短くなり、筐体内でかなり自由に共鳴場所を移動させて響くことができるようになる。
さて、ヘ音記号の五線の下に外れた Ⅳ領域ではどのように響くのか?
IV領域ではチェロは筐体内にその波長(Cでは5.2m)を収納できる独自のルートを持つことができない。波合成シミュレーションと重ねると、おそらく、ミ・ソ・ド・ド等の倍音の合算軌道を利用して基音の 5.2mの波長を得ていると推定される。1オクターブ上のC(131Hz、ルートが存在しない)を含んでいないことが特徴だ。
この4領域と8の字波形ルートは、チェロという楽器(筐体)の普遍的な特徴と思われる。この筐体構造自体あらゆるピッチに対して共鳴できる発明品であることに気づかされる。
実際、arco で演奏される場合は雑音も加わって波形は複雑になっていく。もう一つ大きな影響はエンドピンである。これらの共鳴の基本構成ルートと共振してチェロの響き・音質に影響すると考えられる。